If there's one thing that separates today's machines from their predecessors it's their ability to respond to constantly changing conditions. This lifelike quality derives from electronic intelligence, usually a microprocessor, and an array of sensors that measure what the machine is trying to do in addition to any outside influences that might affect what the machine has to do next.
Unfortunately, one of the most important machine variables, torque, has also been one of the toughest to measure. For lack of a practical sensor, some machines approximate torque from related variables, such as motor current, while other machines ignore it altogether.
This may change, however, as researchers learn more about the effect of mechanical torque on certain magnetic materials. Stress-sensitive magnetoelastic elements embedded in or fastened to shafts and other structural components may one day produce all the torque signals any machine will ever need.
Weighing the options
Producing and controlling rotary motion is one of the most common machine functions. Rotation – whether you're talking about a lathe, washing machine, or a steering system on a car – is usually defined in terms of speed and torque. While today's technology is more than adequate for measuring rotary speed, the same hasn't been true for torque.
Commercial torque sensors fall into one of several categories based on the nature of the interaction between the shaft and sensor. The most common variety, strain gages, measure the local strain on a shaft due to applied torque. Besides being expensive, strain gages require an electrical or telemetric connection to the rotating shaft, and frequent correction for environmental variables.
Another group of detectors, elastic sensors, key on the mechanical twisting that results from torque. Here, a dedicated sensing shaft, or "torsion bar," accumulates an angular displacement between opposite ends. This displacement may be measured optically or by using a pair of magnetic encoders or resolvers. The compliance of the bar, its length, and disproportionately large radii at the ends present functional and packaging problems in most applications.
Surface acoustic wave (SAW) methods are also used to measure torque. SAW sensing systems look for strain-induced changes in the propagation speed of ultrasonic sound within the shaft. The catch is getting the vibration energy into the shaft. It requires putting transducers on a rotating component, and energizing them using radio waves. Making the transducers is also a challenge, as they require extremely tight manufacturing tolerances.
Some torque sensors, early magnetostrictive types, work by measuring stress-induced changes in the magnetic permeability of a special alloy, either attached to or comprising the shaft. This method requires two coils; one to induce a magnetic field in the active area and another to pick it up. Drawbacks arise primarily from the potential for inaccuracies caused by the many other variables that influence permeability, as well as substantial power consumption.
Attractive alternative
Another torque-sensing method that harnesses magnetic interactions is the magnetoelastic type. The key element here is a ferromagnetic ring or shaft section that's circumferentially magnetized. Normally, under no load, the magnetic flux remains inside the ring and, as a result, if you measured the external field, you'd get a reading of zero.
Torsional stress, however, realigns the magnetic domains in the ring, forcing the flux outside. This produces an external field whose polarity and strength correspond to the direction and magnitude of the torque applied to the shaft.
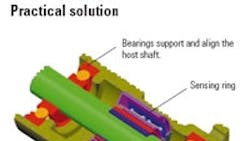
Perhaps the best way to understand how magnetoelastic sensing works is to start with the magnetic sensing ring itself. The ring is made from a highly permeable, magnetostrictive material formed to fit the host shaft. In its unconditioned state, it's magnetically isotropic, meaning the magnetic properties are the same in any direction because individual magnetic domains, or moments, are randomly aligned.
In order to work, the ring must be pressed onto a tapered shaft made from a low-permeability material. The resulting strain induces an circumferential "hoop" stress that clamps the ring to the shaft, while creating a preferred axis of magnetization. Because the magnetic domains may point in either circular direction, the net magnetization in the sensing ring is still zero.
Once the ring is firmly in place, it can be magnetized in a preferred direction, along the circumference, by spinning the shaft-ring assembly in a strong field. Another way to magnetize the ring would be to launch a highcurrent pulse down the shaft. Depending on shaft dimensions, a 1,000-A pulse held for about 10 msec should be more than sufficient to align the magnetic domains.
Continue on page 2
As long as there's no torque on the shaft, the magnetic moments hold their alignment along the circumference of the sensing ring, and the ring's magnetic energy remains inside. In this state, the magnetic flux lines follow a near-perfect circumferential path. The special properties of the ring – the material is permeable and homogeneous – keep the flux in these preferred paths and, consequently, in the ring.
Putting a torque on the shaft, and hence the ring, induces a torsional stress in both components. If the stress were visible, you'd see that it distributes itself in a helical pattern, much as you'd expect a rubber band to wind up if you twisted it along its length.
It turns out that the stress lines present a new preferred axis for magnetization, called an "easy axis." In other words, torque causes the magnetic moments to tilt from their original direction, along the circumference, into the path of the helical stress lines. This, in turn, re-orients the flux, creating an axial component that flows out the ends of the ring.
The escaping flux, and its associated magnetic field, is what makes it possible to measure torque. The greater the torque, the greater the axial flux component, and the larger the external field. At maximum torque, just before the shaft deforms, the field reaches its highest value, corresponding to a maximum magnetic-moment tilt angle of 45°.
Making it work
To get a better feel for the applicability of the new torque sensing method consider the findings of one of the early experiments. The test compares sensing rings made from two commercially available magnetostrictive materials, Permendur and T-250.
Each ring is installed on a stainless steel shaft slightly larger in diameter than the opening in the ring. This method achieves the two things necessary for the transducer to work: One, it establishes a uniform radial force between the ring and shaft, which helps transfer, via friction, all of the shaft torque to the ring. Two, it creates a large circumferential tensile, or hoop, stress in the ring – in the ratio of the ring's inner radius to its wall thickness – which produces the desired anisotropy favoring circumferential magnetization.
The rings are polarized by a circular field produced by a unidirectional current pulse (8.3-msec half-sine, 1,000-A peak) conducted axially through the shaft.
To measure the external magnetic field, two Hall-effect ICs mount near opposite ends of the ring. Their outputs connect to form a difference signal. Because flux passes through the two sensors in opposite directions, the signal from one sensor increases, while that of the other decreases. The difference signal, therefore, is twice as sensitive to the field of interest, but relatively immune to stray fields, which tend to cancel out.
The test setup applies torque through a torque arm fixed to one end of the shaft. By shifting weights from one side of the arm to the other, the system produces a series of clockwise/ counter-clockwise (CW/CCW) torque cycles.
When put through their paces both sensors respond nearly as predicted. For example, the ratio of slopes (output voltage plotted against torque) between the two rings measures 1.83, compared to a calculated value of 1.79. Both slopes are somewhat less linear than expected, however, primarily because of hysteresis. In this regard, T-250 performs better than Permendur, offering -1.06% linearity compared to -3.11%.
The graphs also show no visible sign of saturating at the torque extremes. In fact, according to calculations, the linear region extends an order of magnitude beyond the maximum applied torque to somewhere in the vicinity of 150 N-m. This exceeds, by far, the stress that can be physically transferred from the shaft to the ring by friction alone.
Slippage at the ring-shaft interface is one of the limiting factors in measuring large torque, and is known to be a major source of hysteresis. But perhaps not for long. Researchers are working on better ways to transfer stress from the shaft to the sensing element, focusing on the mechanical geometry at the interface and on methods that incorporate the sensor into the shaft itself.
Will it last?
Stability is a concern for any sensor, particularly one that relies on altering atomic and bulk material states. In the case of magnetoelastic torque sensors, the big question is whether the remanent circular magnetization in the ring will remain stable over time, temperature, and usage.
Simple theory predicts that, when magnetized, the ring is at its lowest energy state; lower even than if it were demagnetized, since a "demagnetized" anisotropic material implies the presence of inherently energetic domain walls. Being at a low-energy state means that there's little energy potential in the system that could possibly react to influences outside the realm of interest.
Continue on page 3
In fact, experiments prove that the sensors are stable over a million torque cycles, including temperature excursions from -55 to 150°C and various types of mechanical abuse.
Understanding magnetoelasticity
Metals, like many materials, are made up of atoms arranged in a crystalline lattice. The lattice structure is cubic with atoms at the eight corners.
There are two variations of this structure. Face centered cubes have six additional atoms occupying the centers of the cube faces, while body centered cubes have one additional atom located at the center of the cube. These regular structures do not repeat indefinitely, but are confined to local volumes called crystalline domains.
Within a domain, the microstructure is regular and repeats, and there are favored directions of magnetism. Usually, these directions are along the edges of the cubic structure, and are called the "easy axes" of magnetization. These preferred axes exist because all of the atomic magnets naturally align within a domain.
Large samples of ferromagnetic metals do not exhibit net magnetization because they are composed of a myriad of small domains. These are randomly oriented and tend to cancel each other out statistically.
Magnetizing a ferromagnetic material, if it contains other metals such as nickel, forces a partial alignment of magnetic domains. The magnetic dipoles interact with their surroundings, namely the crystalline lattice, creating stress and strain and often causing minute dimensional changes. These changes are known as the magnetostrictive effect, and were first reported in 1842 by British physicist, James Joule.
The magnetostrictive effect also works in reverse: Straining a material aligns its magnetic domains. The strain creates a new "easy axis" of magnetization such that the magnetic domains align randomly opposite to each other along the strain axis.
Instead of strain, now consider the stress produced in a material by an applied force or torque. Stress also induces an "easy axis" of magnetization through the strain it produces in the crystal lattice. This effect, defined as magneto-elasticity, is the underpinning of a new torque-sensing method.
Larry Rupert is president of Magna-lastic Devices Inc., a subsidiary of Methode Electronics Inc., Carthage, Ill.