Tuning in and turning on
As control systems expand into networks of axes regulating complex motions, meeting specifications is a growing challenge. If the only requirement is to get from A to B, simple step input is usually sufficient. But for motion systems that comprise multiple axes and require smooth, multi-point motions, controlled input is required. For these complex operations, dynamics are linearized around operating points. From there software-based automatic tuning mechanisms can determine optimal test and performance parameters. Besides accomplishing this more efficiently than traditional tuning methods, automatic tuners alleviate more system resonance problems, increase efficiency, and more finely tune axes for high performance.
Identification
This first step in the “automatic” tuning process is to collect data. To begin, a search is carried out for a low-bandwidth controller that will prevent motor drift during measurements. Then the plant (machine) transfer function is measured using a tight list of frequencies. During this procedure a series of commands at different frequencies are fed to the motor, and the resulting motor responses measured. The plant transfer function can be calculated from measured feedback over the specified frequency range. Because machines that absorb energy may experience harmful vibrations, maximum continuous and peak current must be defined by the user for each application to avoid damage.
Controller selection
This is the second step in the automatic tuning process. The goal is to choose a good linear design that minimizes control efforts and counters sensor noise by producing a low-current command at the machine drive. Controllers must also be sufficiently robust to offset uncertainty. Finally, they must have appropriate gain and phase margins to meet application requirements while not exceeding demands or negatively affecting closed-loop performance.
Some of the control schemes for which automatic tuning must work include:
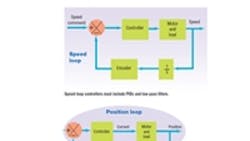
• Speed controllers, which follow a speed trajectory. These controllers include a PI and a low-pass filter. A standard speed controller is usually driven by an external position controller, which is similar to some internal feedback loops. Automatic tuners integrate optional notch filters if needed.
• Position controllers, which follow a position trajectory. These controllers use the position trajectory and its derivative (speed) as the trajectory command. Position controllers must include a PID and a low-pass filter. As in speed controllers, automatic tuners independently integrate notch filters when needed.
• Dual-loop position controllers, which follow a position trajectory with an inner speed loop and an outer position loop. The inner-loop controller is a speed controller, while the outer loop is a simple gain controller or a PI filter.
In addition to having a good linear design, controllers should overcome linear phenomena. One threat is loss of stability or too large an overshoot when the current driving the motor saturates. If saturation occurs, the controller must recover quickly. Another linear phenomenon to protect against is an excessively large and noisy limit cycle. At high speeds, encoders can be used as tachometers to stabilize loaded motors. At lower speeds, this is not possible and results in unacceptable limit cycles. Instead, some systems include time-varying, speed-dependent switching controllers integrated with gain-scheduling algorithms to overcome limit cycle problems.
Test execution
All software must be tested before use, and automatic tuners are no exception. the identified motor (together with user-supplied parameters for current saturation and shaft-angle range) is run to calculate key trajectories in which motor current does not saturate and shaft angle remains within its permitted range. Controlled feedback systems can be tested with square-wave reference commands for speed-controlled systems and smooth-position squarewave reference commands for position or dual-loop systems. Actual controller behavior can be determined by evaluating small and big signals. For small signals, controllers don’t saturate the servo amplifier; smallsignal behavior reveals the full controller bandwidth according to settling time.
Continue on page 2
It usually takes systems much longer to stabilize after larger signals. For this reason, the controller bandwidth is evaluated in large-signal responses as the time between end-of-saturation and final settling. With large signals, the time it takes to stabilize the motor at its required speed or position reflects maximum torque; observing resulting torque waveforms is the easiest way to determine if torque should be clipped at any points.
Automatic tuners can provide trajectory parameters for current boundaries, which can then be used in tests. An end user, for example, may wish to increase the recommended amplitude of the test signals to determine how controllers behave at saturation. A system integrator, on the other hand, may wish to consider friction and load. In any case, automatic tuners assume that the basic system requirement is a fully balanced state in which there is no movement when no current is applied. To use an automatic tuner with maximum efficiency in different scenarios (in velocity, position, and dual-position loops) integrators must ensure system safe operation by providing the following parameters:
• Speed limit: not to be exceeded by the tuner. If the sensor reads a faster speed, an emergency stop is applied.
• Application current peak limit: the maximum current used for short intervals. This value is used during identification and testing as the continuous current limit.
• Application current continuous limit: the maximum current used for ongoing operation. During identification and testing the current never exceeds this value.
• Encoder counts per revolution.
• Negative and positive displacement: the lower and upper limits that define range in which the motor may move. This is expressed in encoder units. The default value used by automatic tuners for both parameters is one revolution divided by the number of electric poles in one revolution.
• Performance: the controlled system’s minimum gain and phase margins. This value is entered in the automatic tuner with a slider, the low end of which indicates large gain and phase margins, and the high end of which indicates small gain and phase margins. Lowering the slider decreases the system’s closed loop performance; that is, a lower bandwidth gives a longer rise and settling time than expected.
• Sensor noise. A wide bandwidth controller selected for higher performance can introduce considerable sensor-based noise in plantmeasured and plant input signals, which may saturate. Incremental encoders generate speed measurement “noise” when encoder slots are not perfectly regular. Resolvers generate measurement noises due to interference of nearby electrical equipment and imperfect grounding. If a controller has large gain at high frequency, it attempts aggressive correction of “errors” it detects through measurement noise. The result is mechanical stress, acoustic noise, and in extreme cases, saturation of the servo amplifier. A sensor noise slider trades closed-loop bandwidth for decreased high-frequency gain.
Analysis
How would one analyze an unbounded shaft angle situation? As an example: A loaded motor with an 8,000 count/rev encoder mounted on its shaft has a continuous current of 3 A and a sampling time of 260 msec. An automatic tuner provides initial test parameters based on the results from the identification/design/ test procedure, and displays these parameters on a computer screen. Assume that expected maximum current during testing will be about half the saturated current (an estimation that may deviate by a factor of two.) For users that decide against using initial test parameters, following is an alternative.
1. Select the velocity. If it’s assumed that a reference step command of VCnt = 5,000 count/sec generates no torque commands greater than the continuous limit, then.
If VCnt is unknown, it must be found through iterations: the first guess can be 10% of the velocity recommended by an automatic tuner in its generated list of test parameters.
2. Bandwidth is the first frequency where gain drops below 70.79% of its dc value; it is the frequency at which the controlled variable’s closed-loop response attenuates 3 dB from a reference. To select other parameters manually, closed-loop bandwidth must be found.
Continue on page 3
Evaluating overall design
A design can be evaluated in either the time or frequency domain. Time domain behavior is also called step response analysis because it is usually determined by the response to step or ramp reference inputs. This evaluation focuses on either speed or position feedback response to sudden change; while not realistic for a typical system — no physical system can track abrupt reference changes, and most servo applications apply traceable reference signals — this method does reveal a considerable amount about dynamic behavior.
Frequency response evaluation is based on the use of bandwidth, phase and gain margins, and rolloff rate to determine the overall system stability.
The main parameters of interest for a step response are
• Rise time: the time it takes feedback to reach 90% of its desired value for the first time.
• Overshoot: the maximum deviation of feedback in the inverse direction of value. When evaluating step responses, it should be noted that although overshoots seem serious, they cannot be in positioning systems. Minimizing overshoot can severely affect tracking ability, but it can safely be done in moderation by profiling the reference command.
• Settling time: the time it takes to reach final stabilization, with a small tolerance about the target.
• Small and large signal response. It is not easy to achieve a “clean” step response for evaluation. Small-size step responses may be severely distorted by mechanical friction, sensor quantization, and other non-linear phenomena such as cogging. For high-gain feedback systems, a power amplifier saturates with very small tracking steps. Large step responses are less affected by friction, but are highly distorted by amplifier saturation.