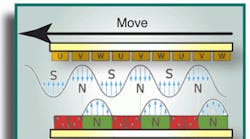
Using linear-shaft motors in parallel

Linear motors are synchronous motors: Current is applied to the coil to form an electromagnet. The coil then synchronizes itself to the magnetic field generated by the permanent magnets in the magnet track. Force in a linear motor is generated due to the relative strength of these magnetic fields and the angle of their intentional misalignment.

One type, linear shaft motors, consists of stationary, cylindrically wound coils and a smooth, nonferrous moving rod; inside the latter is a series of rare earth-iron-boron (NIB) permanent magnets propulsed by attractive and repulsive coil forces. Some of these motors are available with shaft diameters from 4 to 115 mm, and output of less than 1 to more than 36,000 N.

Parallel drives basics

Parallel-drive systems are most commonly utilized in Cartesian or gantry robots. More specifically, these robots use twin, side-by-side drives for a variety of applications, such as: pick-and-place work; glasscutters and sealant applicators; assembly operations; laser engravers and arc welding; and for handling machine tools.

Parallel-drive systems are also found in other motion-control applications:

• High-precision (and ultra-high-precision) single-axis robots are used in optics, microscopes, semiconductor, and machine tool applications. These require resolution and position accuracy in the sub-nanometer to high-picometer range.

• Parallel drives are used in actuators demanding very high force — including material testing equipment and punches.

Building a traditional parallel drive creates certain design challenges: All parallel drives (or gantries) require orthogonal alignment — the ability to keep the parallel axis square. In machinery that utilizes traditional mechanical drives (whether screw, rack and pinion, belt, or chain drive) misalignment or stacked and significantly accumulated mechanical tolerances can cause the motion system to bind and even lockup entirely.

Direct drives suffer from another issue: Problematic sine error (which we'll fully define in the next section) can be introduced if installation is inaccurate or the linear motors exhibit internal variances.

The common solution to these issues is to drive and control each side of the parallel system and electronically synchronize them. This approach, called tracking control, has drawbacks: Cost is higher, as twice the electronics are required (including drivers and feedback) compared to a single-axis system. Tracking control can also introduce synchronization and tracking errors, which degrade performance.

In contrast, linear shaft motor responsiveness simplifies their integration into parallel systems. As with all parallel drive systems, the motors require physical connection with the mechanism, which in turn allows the axis to only move in one degree of freedom. However, dynamic motion generated by two identical linear shaft motors that receive the same control signal is inherently synchronous — so the parallel linear shaft motors act as one.

Linear shaft motors also eliminate force differences that other linear motors exhibit as performance loss and synchronization and tracking errors.

Page 2 of 2

Sine error issue

Consider an ideal scenario: When installed properly, noncontact linear shaft motors are incapable of mechanically binding. The magnets in a linear shaft motor are centered, which renders the airgap dimensions noncritical. The coil completely surrounds the magnet, so force is the net effect of the magnetic field. Any force variation normally caused by airgap differences (from misalignment or mismachining) is eliminated — to simplify alignment and device installation.

In fact, these characteristics are true of all cylindrical noncontact linear motors — so what makes linear shaft motors different from any other design? The answer is sine error — the phenomenon that causes force variations in most noncontact linear motors.

In a parallel drive system, when the separate coils' magnetic fields are perfectly aligned, and the magnetic fields in all the magnetic tracks are perfectly aligned, they in effect become a single motor without any differences of force generation.

On the other hand, any misalignment of coils or magnetic tracks can cause the angle of misalignment of the magnetic fields in the motors to differ, thus producing different forces in each motor. In turn, this force difference can cause binding.

Sine error is the force difference produced by misalignment of coils or magnetic tracks as calculated:

Where F_dif = Force difference between the two coils

F_gen = Force generated

D_dif = Length of misalignment, and

MP_n-n = North-to-North magnetic pitch

Most commercially available linear motors have a north-to-north magnetic pitch of about 25 to 60 mm long; such a pitch is touted to reduce IR losses and improve the electrical time constant. However, a 1-mm misalignment in a motor with a 30-mm N-N pitch causes roughly 21% power loss.

In contrast, linear shaft motors use a much longer north-to-north magnetic pitch to reduce the effect of sine error due to accidental misalignment. Therefore, the same misalignment of 1 mm in a linear shaft motor with a 90-mm N-N pitch results in only 7% loss of power.

Location versus mass center

Pairing linear shaft motors under one control was a setup first used in single-axis robots. Here, it is impossible to position motor and feedback to the exact same location. Instead, accurate positioning can only be executed with feedback that references the workpoint's center of mass. Motor force is also directed at the workpoint's center of mass.

By putting an encoder in the center of mass, and using parallel linear shaft motors equally spaced off that center of mass, an engineer can get feedback and force generation in the center of mass. This is impossible for other parallel-drive arrangements that require two sets of encoders and servo drives.

Detecting center of mass is also a technique useful for gantries. Traditional units have two different motors driving separate ballscrews by different controllers, electronically connected together. (Alternatively, two linear motors with two encoders electronically connect together via two drives.) Now, two shaft motors, one encoder, and one amplifier are sufficient if system stiffness is sufficiently high.

Unified feedback and control is also beneficial in applications demanding extreme forces. Here, any number of linear shaft motors can be connected to achieve a summation of their forces.

For more information, call (540) 633-1677 or visit nipponpulse.com.