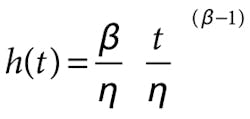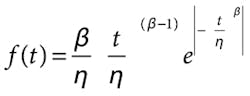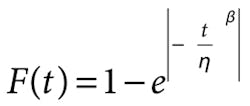Unlocking Weibull analysis

Cumulative Density Function (CDF):

Eta (η) represents the characteristic life of an item, defined as the time at which 63.2% of the population has failed. The shape parameter, beta (β), is the slope of the best-fit line through the data points on a Weibull plot. The variable t represents the time of interest when solving these equations. (See the graph Basic Weibull Plot.) The hazard rate describes how surviving members of a population are failing at a given time. The hazard rate and Weibull shape parameter, beta, have a distinct relationship. ▶ When β < 1, the hazard rate decreases with time (reflecting infant mortality or failures soon after rolling off the production line). ▶ When β=1, the hazard rate is constant over time. ▶ When β > 1, the hazard rate increases with time (population wearout or products wearing out at an increasing rate as time passes). Weibull distributions can also take the form of other statistical distributions depending on their β values. ▶ When β < 1, the Weibull PDF is the same as the gamma distribution. ▶ When β = 1, the PDF reduces to the exponential distribution with a failure rate, λ, equal to 1⁄η. ▶ When β = 2, the Weibull PDF becomes the Rayleigh distribution (failure rate linearly increasing with time). ▶ Data that fall into a normal distribution also generate good Weibull plots, with β ≥ 3.4.

Data types

The accuracy of any analysis depends on the type, quantity, and quality of data being analyzed. There are two categories of data used in a Weibull analysis: time-to-failure (TTF) and censored (or suspension) data.

As the name implies, TTF data indicates how long an item lasts before failing. It can be measured in hours, miles, or any other unit that defines a product’s life. In some cases, the life of different parts of an item may be described by different metrics. For example, on airplanes, engine failures can be reported based on flight hours, while landing gear failures are tracked by the number of landing cycles. Failures in different parts of an item must be treated separately for analysis and then combined to create a system-level life prediction. TTF data should also be associated with a specific failure mode for the part whenever possible. This data can come from various sources, including reliability growth testing, reliability qualification testing, and maintenance databases of field data.

Censored data represents failure data recorded over an operating or test period. It can be broken down into three categories, Right-censored data includes test/operating times for items that did not fail (suspensions) and those that did. Interval data includes all failures within a specific time interval, but the exact time-to-failure is unknown (e.g., warranty data). For left-censored data, the exact time an item failed is unknown, other than the failure occurred before it was discovered.

Although Weibull analysis can be done without considering individual root failure causes, knowing and segregating failure modes lets engineers extract information about the item’s reliability.

A decreasing failure rate (infant mortality or product failing soon after being made) is generally attributed to problems with manufacturing or part quality. It indicates that reliability of the remaining products soon improves as defective items fail quickly and are weeded out. The rest of the items, considered defect free, either fail at a relatively constant rate or at an increasing rate as they wear out. Constant failure rates are common for electronic devices and complex systems due to the large number of different possible failures. Most mechanical item failures, however, are caused by wearout.

Performing Weibull analysis

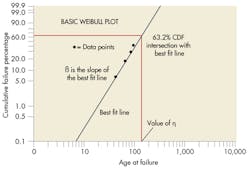
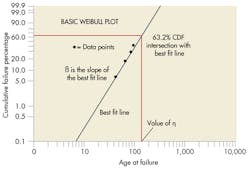
The traditional approach to performing two-parameter Weibull analysis is by plotting the data (usually done using commercial software). Each failure time is ranked based on the number of items that did and did not fail at that time, with the most popular rankings being mean and median. The data is then plotted manually or by software on Weibull probability “paper,” .

Commercial software like WinSmith, SuperSMith, or Quanterion’s QuART-ER, simplifies analysis by automatically ranking and plotting failure data. Tools vary widely in price and can typically be downloaded off the internet.

A best-fit line drawn through the data points lets engineers determine how well the underlying statistical distribution fits the data. If the fit is valid, the best-fit line provides the item’s characteristic life and failure rate over time. If the distribution does not provide an acceptable fit, the Weibull plot’s qualities can identify a more appropriate distribution or suggest a better interpretation of the data. For example, there may be other failure modes, a sudden change in the predominant cause of failures, or items were used in different environments. Plot features such “knees” (corners) or S-Shapes often indicate one or more of these problems may be responsible.

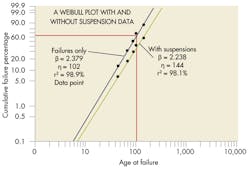
It is critical to understand that even though right-censored data is not plotted as part of a Weibull analysis, it significantly affects rankings that determine the Weibull plot’s shape. Omitting data on items that don’t fail can generate results that underestimate an item’s true reliability. (See A Weibull plot using data with and without suspension.) This can prove costly in terms of more maintenance actions, inventory of spares, and an unnecessary redesign to improve reliability. Analysts should include all pertinent data to ensure accurate analysis results and interpretations.

Assessing the fit

Regardless of the technique used, an analyst must assess the assumed statistical distribution’s fit to a dataset. The failure data plot is particularly useful, as it not only allows for a simple check of whether a linear fit matches the data, but can also indicate potential solutions when the fit is not linear.

Other statistical tests that quantify the goodness-of-fit to particular distributions include the Chi-square, Kolmogorov-Smirnov, and Anderson-Darling tests. Each has advantages and disadvantages, depending on the quantity of available data and the distribution being analyzed. Information on these tests can be found in most reliability and statistics books.

To this point, a good linear fit to a dataset has depended on selecting an appropriate statistical distribution. However, this can be complicated.

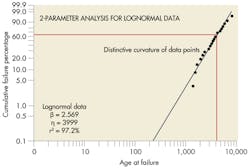
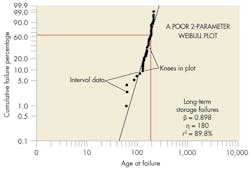
Consider a case in which the failure data were recorded for a single failure mode of a mechanical component that led to a device failure. (See A poor 2-parameter Weibull plot.) The failures occurred in a long-term storage environment and were not discovered until the devices were removed for periodic testing. This particular failure mode was deemed critical due to the large number of failures. Despite the fact most devices worked when removed for periodic testing, suspensions (those that passed the testing) were not recorded in the original dataset. This dataset, then, could not be used to estimate the population’s reliability. Data from this testing can still be used, however, to illustrate different filtering techniques that can improve a distribution’s fit to a dataset.

Because the devices were in storage, failures were not discovered until they were tested. Actual failure times are unknown, so interval (failure discovery) data must be used for analysis. There are also distinctive “knees” in the plotted results, which can indicate several different types of failures, different operating environments, poorly manufactured lots, or parts made by different manufacturers. In this example, the reason for failures was known, storage environments were similar, and all parts were made by the same manufacturer. Consequently, further investigation was needed to identify the reason for the discrepancies.

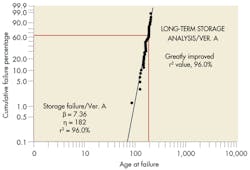
A review of serial numbers of failed parts did not reveal any indications of a manufacturing issue. However, it did indicate that failed parts were from two different versions of the device. Although the mechanical part was identical in both designs, data was filtered by version and an independent analysis performed on the two datasets.

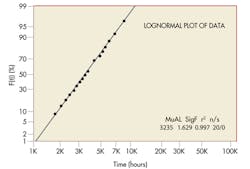
Plotting “Version A” data shows a noticeable improvement in the linear fit to the plot. The high beta value, 7.36, suggests a rapid wearout condition for the failing parts in this version.

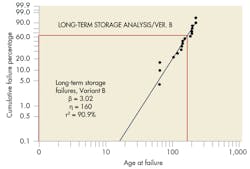
A Weibull plot for “Version B” data (Figure 7) has a best-fit line with a smaller beta (3.02). Though used in two different versions of the same device, the actual part, reason for failure, and storage environment were identical, so there should not be a sizeable difference between beta values for these two datasets.

It was subsequently determined that the difference between the two versions was the test circuitry used to diagnose mechanical-part failures. Thus, failure data for the two designs were based on two different test units. Analysts questioned whether the mechanical part or test circuitry was responsible for the failures.

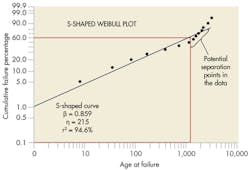
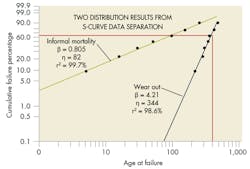
Another problem arises when the Weibull plot creates an S-shaped profile around the best-fit line. It usually means a mixed dataset (See S-shaped Weibull plot). Standard filtering techniques can separate the datasets to get accurate results. This requires identifying the reason why there are different failures in the dataset. It could be:
▶ More than one reason for the failures.
▶ The same reason for failure, but different operating environments.
▶ The same reason for failure, but different part manufacturers or production lines.
▶ Closely grouped set of serial numbers (indicating a bad production lot).
▶ Same type of failures but different reasons.

If you can’t find the reason, you can still try to categorize failures through statistical means. One approach is to assume the datasets are “appended” together with no overlap in failure times. You can test each potential separation point around the main inflection point looking for the best statistical result. The statistical test is based on the goodness-of-fit for the two resulting distributions (See Two distribution results from S-curve data separation).

The goal of a Weibull analysis is to estimate the reliability of an item in a specific application or environment. Results are used to estimate reliability and the adequacy of a design, and for developing maintenance schedules and inventories of spares.

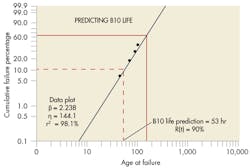
Using statistical analysis, it is easy to predict reliability. Since the y-axis coordinates on the Weibull plot refer to the percentage values of the CDF, the reliability can be determined directly from the plotted dataset.

Once the Weibull parameter values are known, reliability estimates can be calculated using the Weibull reliability function, R(t). The reliability function can also be mathematically manipulated to solve for a reliability/life prediction for an item population. For example, one could calculate a B10 life, which is equivalent to the time when the population’s reliability is 90%. (See Predicting B10 Life.)

Reliability predictions can also be performed on separated datasets, such as those for an item with competing failure modes, operated in different environments, produced by different manufacturers, etc. The prediction requires the use of a scaling function to address the impact of each failure mode distribution on the overall item’s reliability.


Resources
▶ The New Weibull Handbook – Fifth Edition, Gulf Publishing Co., 2007, by Abernethy, Dr. R.B., (http://tinyurl.com/cdrypo9)
▶ Applied Life Data Analysis, John Wiley & Sons, 1982, ISBN 0471094587, by Nelson, W. (http://tinyurl.com/cz4cl39)
▶ Mechanical Analysis and Other Specialized Techniques for Enhancing Reliability – MASTER, Reliability Information Analysis Center, 2012, ISBN 978-1-933904-39-9, by Rose, D., MacDiarmid, A., Lein, P., et al (http://tinyurl.com/cqlyt7f)