Some machines turn on and stay on. Others do their work by successively starting and stopping. Anything beyond 60 cycles/ min is generally considered a high cycle rate, and is capable of exacting a heavy toll on individual components and overall system performance. Some functions have strict speed and accuracy requirements, single-revolution applications for instance, and these can be among the trickiest. But the right combination of drive components – motors, couplings, clutchbrakes, and reducers – can make light work of most any high-cycle application.
System stress
Rapid-cycling applications accumulate a remarkable number of cycles over a relatively short time. Consider that in a month, a 24-hour-a-day 100 cycles/min application will have tallied 2,880,000 cycles. At this rate, standard dry friction clutch-brakes may wear down in as little as five months – less if the rest of the system is not in good order.
Heat buildup brought on by high-cycle rates is another source of distress. Heat results from friction surfaces engaging, and with some forms of clutch-brakes it is also a byproduct of the actuation method. In any case, when accelerating the load, a portion of the horsepower (often half) is converted to heat rather than used for work; thermal horsepower is expended while the clutch goes from partial to full engagement. Upon decelerating, all the power of the moving load is turned to heat; the thermal horsepower required in braking the load.
So as a load is indexed, the clutch brake generates heat. With high indexing rates, heat can build up rapidly. It is particularly so with dry friction units which sometimes necessitate forced-convection cooling. Apart from the fact that nobody wants a red-hot clutch-brake in the middle of their drive train, excessive temperatures can weaken friction materials and accelerate wear.
Beyond concerns of clutching and braking, rapid-cycle operations are notorious for shock loads that continually buffet gears, couplings, and the like. High service factors are in order; all components must be prepared to withstand shock. Also, during torque reversals due to constant starts and stops, having low backlash reduces speed buildup prior to re-engaging, so there’s less impact energy. Torsionally rigid components work best down the line. While rubber-insert couplings, for example, are commonly touted for their damping abilities, with torque reversals they can actually add to the shock, winding up to store energy and springing back to create an impact.
Shaft connections are crucial in a shock-load situation. Quill connections used in clutch-brakes and gearboxes take a beating in high-cycle applications. Standard quill connections have a loose shaft fit, for assembly purposes, and with each indexing move the key is hit with hammer-like force, so it distorts or wears out quickly. Furthermore, it can cause galling, making disassembly a problem. Similarly, slip-fit keyed connections used on coupling and pulley attachments are prone to pounding with each torque reversal, and will fail quickly with the high number of cycles involved. It’s expedient, then, to use tight-fit bores and compression-type connections.
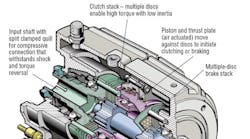
Clutch-brake overview
In many machines, some form of clutch-brake is responsible for disengaging and re-engaging the load, thereby providing incremental motion. There are certain mechanical-lockup clutches that work against a positive stop and do not slip. Wrap spring and so-called “single revolution” clutch-brakes are examples. However, they are generally used only in low-inertia applications where near-instant stops are acceptable. Friction- based units are used in the majority of high-cycle drives.
Friction clutches and brakes can be broken down into several categories. Dry friction devices are based around a steel plate contacting a friction disc, which is a second steel plate bonded with friction material. It is common for these to be cooled by the surrounding air, but such versions have limited heat dissipation capabilities. While many use an open design that allows airflow to the contact areas, the easy access also applies to dust, dirt, and unwanted fluids.
Wet disc or oil shear clutches consist of multiple steel plates mated to friction discs in a stacked configuration. Fluid flows over the contact surfaces and removes the heat, transferring it by convection into the housing, which in turn conducts it to the surface to be dissipated to the surroundings by convection and radiation. Sometimes fluid is circulated through a heat exchanger.
Wet clutches can operate on the oil shear principle or as a standard friction clutch. As an oil shear or hydroviscous clutch engages, fluid shear transmits motion until input and output speeds are nearly equal and mating discs make full contact. Because rubbing between metal and friction material is limited, wear is minimized. The other versions are simply wet disc clutches where the fluid is used as a lubricant and coolant and has little hydroviscous effect.
Electric, pneumatic, and hydraulic are the usual actuation methods for frictionbased clutches and brakes. Of the two fluidic types, pneumatic actuation is far more common in industrial applications. Besides pressure-based fluid actuation, there is also vacuum-based.
Electric units have a magnetic coil that pulls friction surfaces together. These are seen in all sorts of low-tomedium torque applications, including high-cycle applications, and are convenient in many ways. However, there are certain difficulties under high-cycle rates. The magnetic coil generates its own heat. With rapid-fire actuation, the accumulation of heat from the coil can contribute noticeably to that from friction. Furthermore, the electromagnets take considerable time to build and decay, and can limit cycle rates and response time. The larger the unit, the more time required. Common sizes take from 100 to 200 msec for buildup or saturation, and 50 to 100 msec to decay.
Air clutches and brakes use compressed air to push a piston and force the friction surfaces together. Vacuum systems draw in the actuator to bring the surfaces together. Vacuum actuation is limited, however, in the amount of force and subsequent maximum torque it can develop. Neither fluidpressure actuation nor vacuum actuation produces heat.
For numerous reasons, air actuated oil shear clutch-brakes work very well in extreme high-cycle machinery. They generate the least amount of heat from friction and actuation, and the multiple disc arrangement provides high torque with low inertia by adding discs rather than increasing disc diameter. Additional cooling measures such as a fan or coolant circulating through a heat exchanger increase thermal capacity considerably.
Continue on Page 2
It’s commonly believed that electric actuation is faster than pneumatic. This is not necessarily the case. There is a delay to saturation and decay in the electric variety, while the solenoid in an air valve is quite small and can trigger rapidly, though the size and nature of the valve is also a large player. Use 24-Vdc high-watt solenoids for the quickest and most accurate response. With ac solenoids, you may see inaccuracy due to response delays associated with 60-Hz ac power, particularly when running in very high ranges.
When using pneumatic clutch-brakes keep the connecting hoses short or use manifold-mounted valves. Accumulators will improve consistency and enable increased cycle rates. They should be 10 to 20 times the piston volume, with regulators located at the accumulators’ input sides. Properly sized air valves are critically important. Allowing the fullest airflow possible is always desirable, but larger valves may respond slower. A balance is needed between the valve size, valve speed, and CV rating, a parameter relating airflow to valve size. In some cases two smaller valves (as opposed to one large valve) may be the best solution.
Impact of inertia
When discussing rotational inertia, or mass moment of inertia, we are often found in a “vicious circle” or catch- 22 situation: the inertia of the load demands we use larger, more powerful drive components, but the larger drive components increase the system inertia even more – considerably more – thus we end up using a good chunk of the power to motivate the drive train rather than the load. This is particularly a problem when a servomotor is required to do the cycling. The motor itself has to be powerful enough to directly start and stop the load, and its size is a burden in itself. With a clutch, on the other hand, the motor often runs continuously, and need not be as large. In fact, with single-direction rotation it’s often advisable to use higher-inertia components on the input side of the clutch. This way, once the motor gets up to speed, it has plenty of stored energy behind it to drive the rest of the system every time the clutch engages.
In any case, with high cycle rates, managing the inertia is extremely important. A high-inertia system is good for “grinding along” nonstop, and its inability to easily stop may be useful in, say, heavy crushing or cutting machinery with constant one-directional drive rotation. But such a system is unwieldy at best when you try to startstop or reverse it at frequent intervals. And the system components likely won’t handle it for long.
Strategic design can ensure high torque and horsepower while keeping system inertia to a minimum, thereby lowering the power demand and facilitating rapid cycling.
In a rotary component, inertia changes by the square of the diameter, but linearly with the mass. Therefore, keeping the components’ diameters as small as possible is key. Reducing mass while maintaining or increasing the diameter does not minimize inertia as effectively. As an example, hollow shafting may be lighter, stronger, and stiffer than solid shafting of identical material. But because of a larger diameter, the hollow shaft carries a much higher inertia about the central axis. (Similarly, for any object of set mass and diameter, the farther the mass is distributed from the center axis, the higher the inertia about that axis.)
The rotational inertia I of an object around its central axis equates to the mass M and the radius of gyration k (about that axis) by the formula:
I = M k2 (lbm-ft2)
For a solid disc (of uniform density) with radius r, the inertia around the central axis amounts to:
I = (M r2)/2
Now, if you consider that the mass of such a disc changes proportional to its diameter, the inertia will go up by the fourth power of the diameter. This is because the mass itself is a function of density r, thickness t, and the square of the diameter d:
M = ρ π d2 t/4
So if you replace M you end up with d2 d2 in the inertia equation. Such a situation occurs in many rotary components – clutch-brake discs for instance. Therefore it is often accurate to associate a disc-like component’s inertia with the fourth power of its diameter. But this is only appropriate when the mass is directly proportional to the square of the diameter.
Usually, system designers have little say-so about the load inertia, though it is a major consideration in the drive design.
Here are some suggestions for keeping system inertia down:
• High inertia at the input side of the clutch can be useful. After that, keep it low.
• For low inertia, use gear couplings instead of large-diameter rubber insert or flanged disc couplings. As an example, a gear coupling with an inertia of 0.2 lbm-ft2 performs comparably in many ways to a rubber insert coupling with 2.5 lbm-ft2 of inertia.
• Choose a clutch-brake with low internal cyclic inertia, particularly if it is at the high-speed side of the drive, which is usual. Multiple-disc clutchbrakes have a substantially lower inertia than large-diameter single-disc varieties, and provide comparable torque.
• Newer high-strength timing belts require smaller pulley diameters than V-belts or traditional standard timing belts. Using wider belts on smaller pulleys is another alternative.
• Gear trains are often purchased whole, in which case the manufacturer can be contacted to provide the reducer’s inertia. Worm gearing tends to have a lower inertia than, say, helical gearing. Pay attention to proper sizing as well. While high-cycle applications require high service factors, be careful not to oversize lest you pay too great a price in system inertia.
A given component’s contribution to the overall system inertia is largely influenced by the component’s location in the drive train. The inertia of a part is reflected through a torque multiplication device by the square of the device’s ratio. For instance, the reflected load inertia at the input of a 10:1 reducer is 1/100 of the (actual) load inertia at the output side; a 50-lbm-ft2 load inertia is equivalent to 0.5 lbm-ft2 at the motor side. Conversely, a clutch-brake with an inertia of 2 lbm-ft2 will reflect 100 times that through the 10:1 reducer, and is therefore equivalent to 200 lbm-ft2 at the load side. This may be much more than the inertia of the load itself. (In this case it is.)
Inertia at the motor is often the focus, however. The motor handles the reflected inertia of the load and any drive components at the low-speed side, but the actual inertia of all cycling components on the high-speed side. As you can see, the inertia of the drive train components can have a larger impact on motor horsepower and life than load inertia.
Stan Porter is a manager with Force Control Industries Inc., Fairfield, Ohio.