Authored by: Edited by Robert Repas Key points: Resources: |
This was an expression I heard long ago from a statics professor who happened to mention this truth while discussing pulleys. Having spent years in the force-measurement industry, it is an analogy that comes to mind in many applications.
One place where it applies is in the calibration of load cells. As with a rope, pulling a load cell (tension) results in an inherent axial alignment with the force vector. But once you begin to reverse the force and push (compression), the force vector doesn’t necessarily want to remain in line with the object being pushed.
It’s easy to see the rope buckle a compressive axial force, but it’s not so easy to see what’s happening in a load cell. The load cell reacts to the applied force that may or may not be in alignment with its axis. The uncertainty of the measured result can become greater than that of the load cell uncertainty when measured under ideal conditions. Thus, it behooves the end user to understand the challenges of applying load cells in compression and, more importantly, how the reliability of the cell’s calibration data affects real-world measurements.
A load cell is typically a stiff and precise spring that outputs a relatively large electrical signal directly proportional to the force on the device. Applying a force to this spring produces strain that causes small deformations in the load-cell material. These deformations directly transfer to strain gages strategically bonded to the load cell. In turn, the dimensional change of the bonded strain gages produces a resistance change in each individual gage. The cells are typically arranged in a Wheatstone Bridge configuration to produce an electrical output whose polarity depends on whether the load cell is loaded in compression or tension.
The symmetrical construction of load cells helps to linearize the output signal, though the linearity of the force versus output curve does depend on the type of load cell used. The linearity range for off-the-shelf load cells can range from 0.03 to 4% of full scale (FS), with repeatability of 0.005 to 2% of FS.
In the years I’ve worked with load cells I’ve heard questions about accuracy more than any other question. That first look at load-cell specifications can be a little confusing. Typically, load-cell specifications do not call out accuracy, but rather linearity, repeatability, and hysteresis. There are other specifications, but these are the most prevalent in the majority of applications. Seldom do they directly quote an accuracy figure.
Most of us have seen the bull’s-eye diagram which explains the difference between precision and accuracy. A tight cluster of points in an area outside of the center indicates precision without accuracy. A loose cluster of points about the center indicates accuracy without precision and a tight cluster of points about the center indicates both accuracy and precision.
Like any measuring device, a load cell can be extremely precise, but inaccurate; accurate, but imprecise; both accurate and precise; or neither. How precisely a load cell operates depends on its construction. How accurately a load cell operates depends on its calibration.
What is force? If you answered, “Force is mass times acceleration,” you are correct. Of course, the load cell usually measures the force of the mass being accelerated by gravity, which is called its weight. So what is mass? A simple explanation is that it’s a quantity of matter. Universally, the unit of measure for mass is the kilogram and any derivation of it.
Uncertainty of a load cell is a value that sets the FS error of the load cell over its operating range. For example, a 10,000-lb load cell with an uncertainty of 5 lb means that the uncertainty of any reading from the cell is ±5 lb of the true value. If the cell measures a load of 6,400 lb, then the actual true load can range from 6,395 to 6,405 lb.
A load applied in tension to a load cell produces a measurement with low procedural uncertainty attributable to setup error. Therefore, this configuration provides a method to measure the uncertainty associated with a device, without significant procedural uncertainty. In other words, the measurement is inherently less plagued by setup error because the force vectors in tension are self-aligning.
However, compressing or pushing the load cell is another story. It is not possible for reputable load-cell manufacturers to ship new compression load cells that don’t meet specification. If questioned and returned, the manufacturer checks the load cell, usually through recalibration. If the unit does, in fact, meet specification (according to the manufacturer) it is returned, sometimes with a significantly different calibrated output. What caused the difference? Did the load-cell characteristics change in shipment? The answer lies in the calibration process.
Standards that govern force-device calibration include ASTM E74, ISO 17025, and ANSI Z540, the latter two primarily focused on process. ISO 17025 and ANSI Z540 dictate that the procedures used for calibration must be validated and uncertainties determined, but it is ASTM E74 that defines the specific procedure used to determine the uncertainty of calibrating a load cell.
This quantification of uncertainty comes from taking a set of ascending data points in three different rotational positions, typically 0, 120, and 240°. The data are averaged on each point for the three runs and a second-order polynomial is fitted to the averaged data. The curve-fitted data are then compared to all of the respective points to calculate the standard deviation. With the standard deviation known, determining the uncertainty of the measurement is as “simple” as multiplying the standard deviation by 2.4, according to ASTM E74 8.4. Quoting ASTM E74 Note 9, “Of historical interest, the limit of 2.4 standard deviations was originally determined empirically from an analysis of a large number of force-measuring instrument calibrations and contains approximately 99% of the residuals from least-squares fits of that sample of data.”
At first, it may be confusing why the load cell would be rotated from 0 to 120° and finally to 240°, taking a set of data at each position. Since the spherically shaped loading surface of the load cell provides for a theoretical point load, the load cell should load identically at each radial position, regardless of the rotation about its axis.
However, the fact is that there are no such things as perfect geometric surfaces. Also, thanks to contact stress, there are no such things as point contacts, but rather a flat area of contact whose size depends on multiple factors — one of which is force. Rotating the load cell addresses two factors: the repeatability of the load cell and the deviation in the setup from geometrical imperfections and misalignments. If enough setup error exists, one could have an extremely accurate and precise load cell yet calibrate it under conditions that prevent the device from meeting specification.
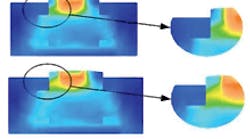
As a load cell is axisymmetrical, it is fitting that the output will only be as accurate and precise as the alignment of the axially applied load. A finite-element-analysis (FEA) study of a typical pancake load cell shows that any deviation from a coaxial load will produce asymmetrical strain with varying load conditions. This will, in turn, produce erroneous readings.
Universal calibration machines that use secondary standards such as load cells or proving rings as the reference for calibration are widely used precision instruments capable of measurements that have extremely low uncertainty associated with setup error. The reference load cell and calibration load cells are usually aligned by special alignment fixtures. In the case where alignment fixtures are not employed, it is possible that an offset could exist between the axes of the calibration load cell and the reference load cell. This will cause a tilt of the stage which, in turn, would cause the force vector to tilt as well. The advantage to this type of calibration system is that the tilted force vector acts upon both the reference and the calibration load cells at the same angle.
However, the tilt could become a source of error because different load cell styles react differently to angular loading. In this case, an ASTM E74 calibration would provide the means by which to quantify this possibly higher procedure-related uncertainty.
To demonstrate this several procedure-related errors were intentionally induced to empirically determine how these errors impact the accuracy and precision of a load cell. A 20,000-lb pancake-style load cell was calibrated per ASTM E74 in compression on a compression calibration system. The manufacturer’s specifications for the load cell under test list a linearity of ±0.10% of FS and a repeatability of ±0.03% of FS.
The data recorded included the following induced errors: no tilt/no offset, offset/no tilt, and offset/tilt. Of course, the no tilt/no offset established the baseline output and uncertainty.
The results show that under coaxial calibration conditions the calculated uncertainty is approximately 3 lb, which equates to 0.015% of the load cell’s full scale of 20,000 lb. Notice this is less than the 0.03% repeatability specification and almost an order of magnitude better than the linearity specification of 0.10%.
Calibrating the load cell with a slight offset produces not only an inaccurate output, but an uncertainty of 0.04% of full scale. Calibrating the load cell with a slight tilt error produces an uncertainty that approaches 0.05%. Both cases exceed the repeatability specification of 0.03%. This would be expected of a “home-grown” type of calibration system, which typically employs an H-frame hydraulic press. These types of systems are plagued with the geometrical errors a universal calibration machine inherently negates.
Users assume a 20,000-lb load on their expensive load cell will nominally produce a 20,000-lb reading that repeats to 0.03% of this value the next time 20,000 lb loads the device. In most cases, the user knows that how the 20,000 lb is applied depends on the nominal reading, and, as previously shown, this reading can change considerably depending on deviations from true coaxial loading. But the fact is that the calibration data received from a manufacturer or calibration service are often inaccurate, supplying values that typically exceed manufacturer repeatability specifications.
This is where process meets procedure. I’ve witnessed large differences in calibration results on the same load cell. While accredited processes address the uncertainties involved in calibration procedures, sometimes the results of procedures tend to drift a bit beyond stated uncertainties. The reason boils down to cost. Conducting an ASTM E74 test on every $500 load cell manufactured would boost the cost of these load cells to over $1,000.
Inaccurate calibration data, in most cases, is not a result of malicious and unethical practices, and ISO accredited establishments have the paper trails that provide a substantiated level of confidence in the their dedication for providing accurate results. But at the end of the day, it is the procedure by which load cells are calibrated, as well as the equipment used in these procedures, that define their accuracy. While universal calibration machines are extremely reliable and do not typically contribute to the procedural uncertainty of a load cell, they are also expensive.
A testing machine like the Force Calibration Machine (FCM) provided by MVProducts and Services Inc. lets users not only provide sanity checks on a load-cell system in-house, but it also lets them ensure the accuracy of its compression-force measurements by calibrating the device as it is being used.
For instance, users may have special fixturing that is removed from a load cell prior to recalibration at an off-site facility. What many users may not know is that load cell accuracy in compression is significantly governed by attached fixturing. A machine like the FCM lets load-cell users overcome this potential source of error through the ability to conform to both procedural and process standards, such as ASTM E74 and ISO 17025. It gives users the flexibility of deterministic calibration on their time and at a small fraction of the cost of a comparable universal calibration machine.
What is a kilogram? However, the evidence is that there’s no reason for the United States force-measuring industry to move to “Traceable to BIPM” declarations versus “Traceable to NIST.” The last comparison of the United States’ primary standard to the BIPM standard resulted in a magnitude of 1 kg —116 μg (yes, that’s micrograms). In other words, when the comparison was made in 1999, it was “identical.” Perfectionists might argue for saying “Traceable to NIST + 116 μg” in order to offset the difference. Typically, it is a universal requirement that users of load-measuring devices and masses need a traceability statement on the calibration to have confidence that the output or magnitude is traceable to the mass standard. This takes place through either a primary standard (mass) or a secondary standard which is traceable back to a primary standard. According to ASTM E74, a load cell is considered a secondary standard except for those exceeding 1 million pounds. This is because the maximum primary standard happens to be the 1 million pound deadweight machine, located at NIST. |