Servo systems do a great job controlling motion, responding quickly to commands, while selectively rejecting disturbances. But to achieve good results, servo gains have to be tuned – a process that requires time and skill. One thing that makes tuning difficult is that it depends heavily on load inertia. When the inertia changes, as is frequently does in many machines, a well-tuned servo system can all of a sudden become sluggish or even unstable.
Load inertia can vary for any number of reasons. A motor moving a work piece, for example, will see an abrupt drop in inertia when the object is released. In web-handling applications, the inertia of the roll drive increases as material is added. In robots, shoulder motors experience inertial changes as the elbow extends and retracts the arm. Although such changes are easy to anticipate, what surprises many servo designers is that inertia acts like a servo gain; when it varies, servo dynamics can change dramatically.
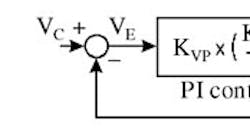
Consider a typical PI velocity loop, consisting of a proportional gain KVP and an integral gain KVI. The controller’s job is to produce the commanded current IC from the velocity error VE. The actual current produced IF is usually close enough to IC to ignore any differences.
The control current drives the motor through the torque constant KT and the inertia J. Notice that the term for inertia appears in the denominator of the motor model; it diminishes (divides) the effect of the current in a manner similar to the way KVP amplifies it. In fact, inertia J acts as much like a servo gain as does KVP.
Although our discussion focuses on a velocity controller because of its simplicity, the effects of inertia variation are nearly the same in more complex control loops such as position and tension controllers.
Fortunately, there are several ways to deal with changing inertia. One is to use a larger motor. If the motor inertia is large, it reduces the impact of load variations. This is because inertia’s effect on stability is based on the relative change of total (motor and load) inertia.
Consider the step responses on the next page. Assuming a motor inertia of 0.0002 kg-m2 and an initial load inertia of 0.0018 kg-m2, a 10:1 (0.002 to 0.02 kg-m2) inertia change implies that load inertia was increased to 0.0198 kg-m2. A larger motor, say 0.002 kg-m2, would have reduced the relative increase to (0.002 + 0.0198)/(0.002 + 0.0018), a factor of 5.7, which is nearly half of 10.
Another way of dealing with inertia variation is to use gain scheduling, a technique where the servo gains are increased in proportion to total inertia change. For example, were the gain KVP raised by the amount that the total (motor and load) inertia changed, there would be no change in the dynamics of the control loop. This would negate the effect of varying load inertia.
Gain scheduling is relatively easy to implement with digital drives – provided the load inertia can be predicted – and is quite common in industrial control. More often than not, a machine controller knows the inertia of an object it’s moving, or it can measure it, as in measuring the changing diameter of a roll accumulating material. In such cases, servo gains (here, just KVP) may be calculated by the controller or PLC and adjusted accordingly in the drive.
There are limitations, however. First, the resolution of the position feedback device (see Tune-up, July 1999) may not be able to support the highest gains, which occur with the highest values of load inertia. Second, mechanical resonance may limit the maximum gain (Tune-up, Oct. 1999, Feb. 2000, March 2000). Both of these problems are avoided by tuning the system with the maximum load inertia so that the system is fully characterized with the highest servo gains.
Explore inertia’s effect on system dynamics
Want to learn more about inertia variation? Then log on to www.motionsystemdesign. com and download this month’s ModelQ simulation program. Launch the program, select “May 2000 Varying Inertia” from the combo box at top center and click “Run.”
You should be looking at the well-tuned system we previously discussed. Now, click in the box on the left next to “J” (total inertia). Type in “0.02” and you’ll observe the overshoot and ringing as shown below. Now schedule the gain: Click in the box next to “KVP” and set the value to 7.2 (up a factor of 10). Notice that the original dynamic performance returns.
You can experiment further with inertia variation on your own. For example, reduce the inertia and see what happens to a system with a gain of KVP = 0.72. It becomes unstable when the total inertia falls below about 0.0002 kg-m2. You can also adjust the gains KVI and KVP so they can better tolerate inertial changes. Generally, lower gains are more forgiving.
George Ellis is a Senior Scientist at Kollmorgen Inc., Radford, Va. His new book, “Control System Design Guide,” 2nd edition, will be published this month by Academic Press. He can be reached at [email protected].