Maximizing efficiency with encoders

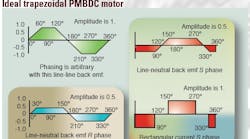
Ideal trapezoidal back-EMF motor

PMBDC motors were first described in the 1950s as three-phase, wye connected, trapezoidal back-emf motors with line-neutral back emf/torque functions. In this model, reference R phase remains at +0.5 for 120 electrical degrees until at 150° electrical. Then it decreases linearly to normalized value -0.5 at 210° electrical. Finally, the R phase remains at -0.5 for the next 120 electrical degrees until 330° electrical, when it rises linearly back to zero. In this way, it completes one electrical cycle over 360° electrical.

In the same interval, both S and T phases (see Fig. 1) undergo the same cycle, but shifted ±120 electrical degrees relative to the reference R phase. Hence, combining back emf/torque functions for a given phase pair using an arbitrary phase reference gives the line-line torque function in the upper left of Fig. 1. Notice that during one 360-electrical-degree cycle, line-line back emf for each phase pair is ±1.0 during two 60-electrical-degree intervals, with a total of six such intervals when all three-phase pairs are combined.

Ideal six-step drive

In combination with an ideal trapezoidal motor, Fig. 1 also shows what's called the “ideal” six-step drive. Below each line-neutral back emf/torque function is a switched dc current supplied to that particular phase — which spurs clockwise rotor rotation. Notice that for the R phase between 0° to 30°, 150° to 210°, and 330° to 0°, current is zero; at 30° to 150° and 210° to 330° its normalized current value is ±1.0.

During each ±1.0 R-phase current interval, either S or T is supplied with a ±1.0 current value so that during each 60-electrical-degree interval, two thirds of the winding is active: In other words, current is +1.0 in one phase, -1.0 in the second, and zero in the third. Combining all three phase pairs produces a six-step current switching sequence during each 360-electrical-degree cycle of T-S, R-S, R-T, S-T, S-R, T-R. In this way, the three phases work to produce constant, normalized 1.0 torque output (shown at the bottom of Fig. 1.) Counterclockwise rotation is made with the opposite current switching sequence: R-T, R-S, T-S, T-R, S-R, S-T.

Electroniccommutation sensor

A simple six-step drive can be built with a double-stack, six-pole rotary switch connected between a battery and PMBDC motor. As one manually rotates the switch either CW or CCW, the motor output shaft synchronously follows the switching action. However, manually rotating a switch to produce continuous output motion is not practical and certainly no improvement over the brushes and commutator used in a PMDC motor. Furthermore, there is a limit as to how fast one can manually rotate a switch to generate motor velocity greater than a few rpm.

In real industrial applications, an electronic commutation sensor instructs the drive when to electronically commute current supplied to each phase pair. Recent advances in electronics have also created sensorless operation of PMBDC motors, but this design is typically limited to non-servomotor applications — automotive and HVAC cooling fans where position, speed control, and torque output are nonissues.

Hall switches

The first electronic commutation sensors used with six-step drives are Hall switches — Fig. 2. Usually, there are three of these switches mounted on a printed circuit board and physically spaced 120 electrical degrees apart from each other, and close to a Hall rotor.

The switch itself is a magnetic semiconductor device that utilizes the Hall effect discovered in 1879 by Edwin Hall. Each Hall switch is turned on and off in sequence by a separate permanent-magnet Hall rotor with the same pole count as the motor rotor. As the Hall rotor rotates, each switch electronically provides commutation signals to the drives control electronics that in turn sequentially switch the drives output transistors (typically IGBT) on and off. In this way, six-step electronically commuted current is made in the motor.

Where three Hall switches replace two-stack, six-pole mechanical switches, PMBDCs produce more continuous, unidirectional output motion like a PMDC motor, but without brushes or commutators.

Even so, Hall switches do have limitations. One major issue is positional inaccuracy of commutation signals that prevents generation of ideal six-step current (of Fig. 1.) Any departure from ideal 0° ±120-electrical-degree spacing between Hall switches causes a corresponding phase current position error — plus imperfect motor output as inconstant torque with ac ripple.

There are two main sources of Hall-switch position error. The first is the physical location of each switch. Hall switches are discrete electrical components, the size of a small ceramic capacitor. Although the printed circuit board to which they're mounted can be positioned to adjust 0° R-phase reference, it's often difficult to obtain perfect 120° spacing between the other two switches. Positioning error of ±5 electrical degrees for S and T-phase switches is common; error is even higher for motors with more than two rotor poles, due to the ratio between the motor's electrical and mechanical degrees. Second, even if all three Hall switches could be evenly spaced, it's impossible to magnetize the Hall rotor with perfect 180 electrical-degree poles.

The Hall rotor is a separate permanent magnet structure that has the same pole count as the motor rotor: See Fig. 2. Typically, this rotor employs a one-piece rubber or epoxy-bonded ring or cylinder in its own magnetizing fixture. Magnetizing the outer surface of this ring or cylinder with more than two 180 electrical degree poles perfectly is impossible. Even using discrete magnets (instead of a single piece) introduces tolerances and magnetic leakage on the rotor. Even if were possible to space magnets or magnetic regions perfectly, the commutation signals supplied to the drive electronics are imperfect. The result: Out-of-phase six-step current that degrades torque consistency and power efficiency.

Commutating optical encoders

Absolute and incremental optical encoders became commercially available in the 1960s. Initially, optical encoders were used almost exclusively as position and velocity feedback devices for PMDC and PMBDC motors. Now, 100 to 10,000 line-count incremental optical Hall encoders are also used for Hall commutation signaling to six-step drives. Today, these are called commutating optical encoders; one is shown in Fig. 3.

Optical Halls eliminate position and phasing inaccuracy, holding to within ±0.5 electrical degrees (compared to ±5° typical for discrete Hall switches.) There is no separate Hall rotor or its associated errors, so commutating optical encoders provide more accurate commutation signals — so drive controls supply more ideal six-step current. What is more, additional position and velocity information from a 2,000 to 10,000 line-count optical encoder can be used by the drive to advance the current phase more accurately, for better torque and power efficiency from PMBDC motors.

Lets get real: Six-step current

Up to this point, we have assumed that if a drive's control electronics is supplied with “ideal” commutation signals then the resulting switched dc current supplied to each phase pair perfectly follows the input commutation signal. In reality, this is impossible. A motor's electrical winding has finite electrical inductance and resistance, so at the beginning and end of each 60° commutation interval, both the rise and fall of each phase-pair current lags behind the input commutation signal.

Basic circuit theorems prove that when a step-input voltage V is supplied to an electrical winding having both inductance and resistance L and R, the resulting current cannot instantaneously rise from zero to V/R-amps. Likewise, when voltage is cut, current cannot instantaneously fall from V/R-amps to zero. Instead, inductive reactance causes each phase current to rise and fall exponentially with an L/R time constant.

Therefore, even though a commutating optical encoder can supply a drive with ideal commutation signals, real six-step current lags input signals. As mentioned, any deviation from the ideal waveforms reduces PMBDC motor torque output and efficiency.

Current phase advance

As mentioned, a PMBDC motor can only output maximum torque and efficiency when its drive keeps each phase current in phase with the motor's corresponding back emf/torque functions. Real six-step drives introduce phase lag in the current — so unless a drive can compensate, the motor outputs less than its maximum continuous torque. Incorporating phase advance into a drive's current control electronics is not difficult, so long as the rotors commutation sensor provides accurate position and velocity information.

In the second and final installment of this series next month, we will show how accurate velocity information is key to getting maximum motor performance — and just how commutating optical encoders provide both.

In this installment

• Brushless dc motors
• Models and ideal operation
• Feedback and sensor options

For more information, visit www.renco.com.