Faster, smaller, and smarter is the mantra of today's servo-controlled machines. As a result, end users have come to expect more and better performance, forcing designers to continuously improve equipment. That said, expanding a machine's servo performance can be challenging because so many factors come into play, including servomotors, feedback sensors, and servo drives, not to mention the mechanical transmission.
Servo performance directly affects the quality of parts that a machine makes and the time it takes to produce them. For example, positional inaccuracy in a servo often translates into dimensional variation of parts produced in cut-to-length applications, and registration inaccuracy in printing applications. System smoothness — or lack thereof — affects the variation of coating thickness in coating machines and part finish in polishing applications. Response time affects the rate of production: The fastest servos cut more plastic bags, print more labels, test more blood samples, and assemble more printer cartridges in a given amount of time. Yet while servos clearly affect machine performance, it's not always easy to translate “what the servo does” to “how the machine operates.” Three key measures bridge those concepts:
Accuracy — how close moving parts settle versus commanded position or velocity
Response — how fast the motion tracks the command
Robust stability — how reliably the motion tracks the command under various operating conditions
Accuracy
Accuracy is usually quantified in two ways — settled-position error and cyclical error. Settled accuracy, the positional accuracy of the servo when it's settled to a commanded position, is straightforward: Errors in servo system position translate to dimensional tolerance buildup. For example, if the cut-to-length servo in a bag machine has a position error of ±0.01 in., it will probably contribute a variation of 0.01 in. to the bag length. The feedback device largely determines settled accuracy. Sine encoders are the most accurate feedback devices with errors measured in arc-seconds, but they can be expensive. In contrast, resolvers and digital encoders are less costly, but have position errors an order of magnitude larger.
The second type of accuracy — cyclical error — is more complicated. When a motor turns at constant speed, position errors translate into an apparent velocity ripple. This ripple repeats during every revolution of the motor, hence the name cyclical. The apparent velocity ripple on the feedback signal feeds the velocity loop, which creates current to compensate for that ripple. Unfortunately, that current creates actual velocity ripple. The result is often a loss of smoothness at speed and an increase in audible noise and motor heat. The fix: Higher-accuracy feedback devices cure cyclical error. Sine encoders have so little cyclical error that they often produce no measureable effects; the same cannot always be said of resolvers and digital encoders. The key for machine designers is to select the right feedback device for each axis of motion.
Mechanical transmissions can also contribute to accuracy problems, because most machines rely on motor feedback as the primary position signal. If a motor connects to the load through a gearbox, the positional error of a gearbox causes the motor feedback signal to vary from the load position.
Transmission components such as lead screws, gearboxes, and belts and pulleys all contribute to error between motor and load. Many of these problems can be adequately addressed by selecting high-quality transmission components. However, for machines that demand the highest accuracy, designers can consider two other solutions.
First, a secondary feedback device can be placed on the load side of the transmission. For example, a linear glass scale can be added to a screw-driven gantry to eliminate accuracy problems in the screw. The motor feedback device can still be used to improve performance if the servo drive supports dual loop — a servo configuration where both motor and load feedback are used simultaneously. The need for dual loop is created because the mechanical compliance between motor and load can severely limit the servo performance when only a load-side position sensor is used.
While dual-loop solves many problems caused by load inaccuracy, the best solution is a direct-drive system, which eliminates the transmission altogether. In direct-drive systems, the motor is directly coupled to the load, significantly improving accuracy — to 10 times better than that of traditional systems, and 40 dB quieter. Other measures, such as servo response, acceleration rates, and reliability also can improve dramatically. For the most demanding servo applications, direct drive is the final step of evolution for the mechanical design.
Many of the alternatives discussed here have implications for the servo drive. When solving accuracy issues, engineers must consider several components, including feedback device families, motor type (standard or direct drive), and the servo loop (support of dual loop).
The servo drive
To improve system performance, the drive must also be considered. Flexibility in support of feedback and motor types provides more options for accuracy issues. Other areas of flexibility include a wide range of servo algorithms, support of multiple communication buses, and a range of voltage and current models. By choosing a family of drives that can support the widest range of options, a given servo system can be used in myriad applications and can handle servo performance issues.
Not surprisingly, a key function of the servo drive is the execution of servo algorithms. Many position/velocity loop architectures are used in modern servo systems, such as integrating position loops vs. integrating velocity loops. In both cases, high servo gains generally contribute to faster response to both commands and disturbances. However, the placement of the integrator can favor different applications. For example, integrating position loops are often used when following error (the position error during a move command) should be minimized. On the other hand, integrating velocity loops are often used when the fastest response is needed.
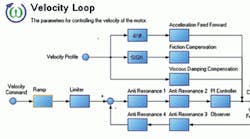
Another family of functions that can help improve servo systems is feed-forward. Feed-forward gains are added paths that speed response to command signals. Servo loops function by minimizing error: More position error generates a larger velocity command, which closes the error more rapidly. But loops take time to respond. In contrast, feed-forward is nearly instant and so allows the servo machine to respond much faster.
Consider the effects of gravity on an overhung load such as an unbalanced vertical axis with a brake. If servo loops are enabled without feed-forward and the brake is released, initially the current command is zero, so the load falls a little. As the servo has time to react, current increases and the axis is eventually restored to the position where it was when the drive was enabled. However, the observer sees a momentary drop. With offset feed-forward, the user can tell the drive how much current is required, and the servo loops can be preset to that value before the brake releases. That way, when the brake releases, the load barely moves.
Current offset is just one type of feed-forward; other types include acceleration, velocity, viscous damping, and Coulomb friction feed-forward. All of these functions share a key characteristic: The drive calculates the ideal response and adds auxiliary signals to the loop paths so that the output responds much more quickly to expected disturbances than a servo loop without feed-forward. Of course, feed-forward gains are no substitute for high servo gains: All demanding applications require high gains to achieve rapid response. However, feed-forward improves even the best-tuned servo loops, working with the loops to provide the most rapid response possible.
Compliance and stability
One area that limits many servo systems is mechanical compliance — the flexibility between motor and load. Transmission components such as gearboxes and lead screws are not nearly as rigid as they seem, particularly at the high frequencies of servo operation. In fact, they act very much like a damped spring between the motor and load. That “spring” makes high servo gains hard to achieve. Why? From the motor's perspective, the load looks different at low frequency than it does at high frequency.
Because this topic is unfamiliar to many engineers, following is a simple example to demonstrate the problem.
Imagine suspending an ordinary office stapler with a large rubber band. If you move your hand up and down slowly, the stapler follows your hand and the inertial load your shoulder feels is your hand plus the stapler. But if you move your hand rapidly, the stapler becomes almost stationary and the inertial load your shoulder feels is, more or less, your hand. In effect, your hand disconnects from the stapler at high frequency. For a servo system, the same thing happens when the motor (like your hand) tries to move the load (the stapler) through the transmission (the rubber band). At low frequencies, the total inertia is the motor plus the load; at high frequencies, the motor disconnects from the load and the inertia is, more or less, the motor.
This disconnect causes serious problems for servo loops. The standard PI or PID servo loops are constructed to control a fixed inertial load. When the load varies with frequency, the loop gains often must be reduced in order to achieve a stable response. When that happens, loop performance falls, sometimes dramatically.
The initial solutions to compliance are mechanical in nature, with two main alternatives available. The first is to reduce compliance by using stiffer transmission components, such as servo-quality gearboxes, lead screws, and couplings to minimize compliance issues. The second is to match the inertia of motor and load: That way, when the load disconnects from the motor, the total inertia changes only by a factor of 2:1. (Note: If the load is 10x the motor, the total inertia goes down by a factor of 11:1 at high frequency.) Although these solutions are adequate, they have limitations. A transmission can only be so stiff before costs start getting out of hand, and increasing the motor size reduces acceleration and increases cost.
At this point, designers can turn to advanced anti-resonant servo algorithms to further improve performance. Anti-resonant algorithms are velocity-loop filters configured to vary servo loop response across the frequency band. Recall the stapler example where the servo loop experiences a total inertia that varies with frequency — large at low frequencies and small at high frequencies. The filters change the frequency response of the loop to compensate for that variation. Many alternatives exist for filter construction and placement in the loop. The simplest structure is to have a low-pass filter or two in the feedback path. Such filters are easy to use, but limited in the amount of improvement they can provide. More advanced filters include notch filters (those that attenuate a narrow band of frequency) and higher order filters, which attenuate more rapidly with increasing frequency. The most flexible filter is the bilinear-quadratic (bi-quad) filter, a design that can be configured as a low pass, notch, or any number of other filter types.
A word on auto-tuning
Even with all their advantages, it can be difficult to find the optimal configuration for anti-resonant filters. Another tool with which servo machine designers should be familiar is auto-tuning. This tool sets servo gains automatically, providing fast and reliable servo tuning even for complex mechanics. However, not all auto-tuning algorithms are created equal. Many don't configure anti-resonant filters or feed-forward gains. In fact, the simplest auto-tuning algorithms excite the load at low frequency and then set up the servo loops assuming a complete absence of compliance. That works well in a lab, where motors might be driving a steel wheel, but results in real applications are usually disappointing. When selecting a servo drive, choose one with an auto-tuning algorithm that covers all the applications in which the drive will be used. If the algorithm is robust, it will save time and provide the high gains that lead to superior servo performance.
For more information, visit kollmorgen.com or call (540) 633-3545.
Savvy servo selection
Improve accuracy
- Select a more accurate feedback device
- Install a secondary feedback sensor on the load side of the transmission
- Use direct drive motors
Improve response time
- Increase servo gains
- Use advanced servo algorithms
- Use feed-forward algorithms
Achieve optimal tuning
- Select a drive with advanced tools such as a dynamic signal analyzer to create Bode Plots
- Select a drive with a capable auto-tuning algorithm
Improve resonance problems
- Make the machine stiffer by using better transmission components
- Eliminate the transmission altogether by using direct drive motors
- Use advanced anti-resonant filters